ホーム >

ブログテーマ >

受験 >

高校受験

このテーマに投稿された記事：3865件 | このテーマのURL:https://jugem.jp/theme/c40/1004/

Tweet
Check

: 高校受験(入試)について、今日は説明会行ったとか入試結果など、高校受験の話題に関わっていれば些細なことでもOK(・ω・)
: 作者のブログへ：「yunnyunn」さんのブログ
その他のテーマ：「yunnyunn」さんが作成したテーマ一覧(5件)

このテーマで記事を投稿する

共通テスト☆バラす『英語』３

JUGEMテーマ：高校受験みなさん、こんにちは。昨夜は、熊本でオールスター☆☆☆ 子供たちの屈託のない笑顔、たくさん見れてよかったです。やはり、憧れや夢って、世界を照らしてくれますよね。では、本日は、いきなり始めちゃいます。共通テスト☆バラす『英語』今日は、❹対話文を解体♪ 配点は、ずっと１０点。出題パターンも、変化なし。ここでポイントになるのが、英作文です。配点が、２点×２あります。...

熊本職業的家庭教師の『見えざる手』 | 2018.07.15 Sun 12:20

JUGEMテーマ：高校受験みなさん、こんにちは。お天気は、曇りっぽいですが、今日も暑いですね。で、実は昨夜・・・生徒さんのお父さんに、「先生、１時間くらいいいですか？」といきなり。・・・今後の勉強のことかなっ？と思いきや、「いい店あるんで、街までね」断る理由もなく、しかも、頭ん中、もービールでジュワー☆ ・・・お伴いたしますいそいそと夜の繁華街へ。フライデイナイトは、人が多め。連れてかれたお店で、『安全地帯』な感...

熊本職業的家庭教師の『見えざる手』 | 2018.07.14 Sat 13:30

共通テスト☆バラす『英語』

JUGEMテーマ：高校受験みなさん、こんにちは。毎日暑いですね。なぜか、扇風機をダブルで回してます。２機だと、風が濃い～ですが、向きのバランスで落ち着かねぇーさて、共通プレテストって、今日あたり！？時間配分は、どうでしたか？英語は、❻まで読めましたか？まあ、この点数が始点となって、入試へのベクトルが形成されるわけで、生徒さんひとりひとりが、いろんな向き、大きさ(勉強の質と量)を抱いて、 ...

熊本職業的家庭教師の『見えざる手』 | 2018.07.13 Fri 15:07

埼玉県高校倍率

埼玉県の県立高校の倍率について、平成30年のデータが掲載されています。 →こちら全高校の平均になりますので、個々の高校については偏差値、人気によって異なってきます。 JUGEMテーマ：高校受験

埼玉県の高校情報 | 2018.07.12 Thu 07:59

リーズナブル

　「リーズナブル」　「国語の解答って、いい加減だと思います！」私のところに詰め寄ってきた教え子がいます。成績優秀な生徒さんです。英語と数学の成績は抜群で、本人も「得意です」と自負しています。そんな中で「国語の成績には納得がいかない！」ということなのですが。「国語の読解問題で、傍線部の理由を答えさせたりする場合、数学のように証明ができないじゃないですか。それって数学と違って国語はいい加減だということになると思うのですが、違いますか！」ドキリとさせられる鋭い質問です。単に成績が振...

文の会ブログ | 2018.07.06 Fri 11:30

某サイトに掲載されているある入試問題について?

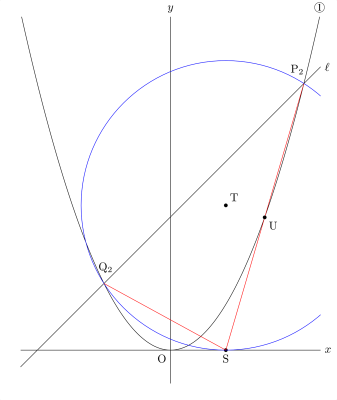
JUGEMテーマ：高校受験先日提示した問題について，(2)(ii)の設問が適切かどうか検討していきます。 ※ \(t\) 秒後の点P，Qの位置をそれぞれ \(\mathrm{P}_t\)，\(\mathrm{Q}_t\) と表すことにします。某サイトによる方針と解答 2点 \(\mathrm{P}_2\)，\(\mathrm{Q}_2\) を通り \(x\) 軸に接する円を考え，この円と \(x\) 軸との接点をSとする。このようにSの位置を決めると，直線 \(\mathrm&#...

SAS 数学教室 | 2018.07.05 Thu 17:59

Kostenlose Uhr Big Sonia Öffnen Torrent Ohne sich zu registrieren Ohne Registrierung PutLocker

⟱⇓⟱↡⟱▼⇩⬇▼⬇▼▼⬇⇩⇩↡↓▼⇩⇩▼⟱ ➡ ANSCHAUEN / RUNTERLADEN Big Sonia ⇐ ⇑↟⬆⇧⇑⬆⬆⇪▲↑⇪⬆↟↑↑▲⟰⬆↑⇪▲⬆ (2018) EngLIsCh Full MOvie OnLIne KostenloSer DOwnload. Hier haben wir das beste Web-Portal, um Filme online zu sehen, ohne Registrierung oder irgendetwas benötigt.. Kost...

Jason | 2018.07.02 Mon 21:56

某サイトに掲載されているある入試問題について?

JUGEMテーマ：高校受験昨日提示した問題について，前回の(1)の解き方につづいて，(2)(i)の解き方を示しておきます。実は，この設問も，問題文がなんとなく気になります。問題文の「このとき」というのは，動き出してから2秒後のことだと解釈していいんでしょうか。私としては，「このとき」というのは，その前に書かれているSの位置の説明，P，Q，Rが動き出して2秒後に∠PSQが最大になったという状況の説明を受けて，「こういう状況設定のとき」というように読めて，「このとき」というのが「∠PSQが最大になったとき（つまり...

SAS 数学教室 | 2018.07.01 Sun 20:32

某サイトに掲載されているある入試問題について?

JUGEMテーマ：高校受験昨日提示した問題について，まず，(1)の解き方を示しておきます。「3点P，Q，Rが一直線上に並ぶとき」ですから，方針がいくつかありますが，すぐに思いつくのは次の2つでしょうか。直線PQの式を求め，それがRを通るような \(t\) の値を求める。直線PRの傾きと直線QRの傾きが等しくなるような \(t\) の値を求める。中学生なら，上の方針をとることがほとんどだと思いますが，直線PQの傾きや切片の部分が文字 \(t\) を含む式になるため，公立入試の対策しかしていな...

SAS 数学教室 | 2018.07.01 Sun 16:35

某サイトに掲載されているある入試問題について?

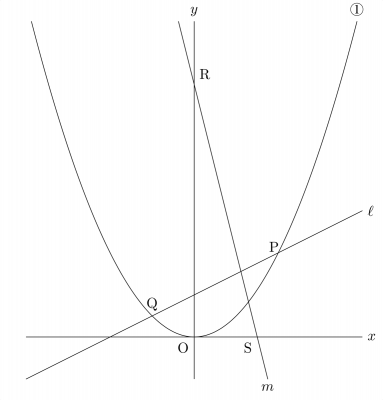
JUGEMテーマ：高校受験久しぶりに，高校入試数学の話題です。実は，かなり前から，某サイトに掲載されているある入試問題が気になっています。あえてサイト名やリンクを掲載しないのは，気になっている理由が，「解答が間違っている」のか，あるいは「問題の肝心な部分を（そうとは気づかず）改変してしまっている」ように感じるからです。まずは，その問題を見てもらいましょう。某サイトに掲載されているある入試問題関数 \(\displaystyle y=\frac{1}{2}x^2\) のグラフにおい...

SAS 数学教室 | 2018.06.30 Sat 22:43

このテーマに記事を投稿する"